MATLAB
MATLAB
1.matlab的基本数据单位是矩阵
2.打开帮助文档命令 doc
打开帮助函数命令 help lookfor
help find
lookfor find
3.通信系统组成
信源(发送信号)->发送设备->信道->接收设备->信宿(接收信号)
4.信号分类
恒参数系统、变参数系统、时变系统、无记忆系统、记忆系统,按照网络层次系统分类分为:网络层、链路层。
网络层指标:吞吐量、响应时间、资源利用率
链路层指标:比特错误率、传输速率
5.模拟通信的特点
设备简单、占用频带窄、通信质量、抗干扰能力和保密性能等不及数字通信。
缺点:
1.保密性差
2.抗干扰能力弱
3.设备不易大规模集成化
4.不能满足飞速发展的计算机通信要求
6.数字通信特点
1.抗干扰能力强、没有噪声积累、可以进行远距离的传输并能够保证质量;
2.能适应各种通信业务要求,便于实现综合处理。
3.便于采用大规模集成电路实现。
4.容易进行加密处理,安全性更容易得到保证
7.常量
变量名 | 描述 | 示例 |
ans | 默认结果变量。当您没有为操作结果指定变量时,MATLAB 会将其存储在 ans 中。 | 2 + 3 (结果存储在 ans 中) |
pi | 圆周率 piapprox3.141592653589793 | circumference = 2 * pi * radius |
eps | 浮点相对精度(机器 epsilon)。表示 1.0 与大于 1.0 的下一个浮点数之间的距离。 | eps (通常约为 2.2204times10−16) |
realmax | 最大双精度浮点数。 | realmax (通常约为 1.7977times10308) |
realmin | 最小双精度浮点数。 | realmin (通常约为 2.2251times10−308) |
inf | 无穷大。例如,除以零。 | 1/0 (结果为 inf) |
nan | 非数值(Not-a-Number)。例如,0/0 或 infty−infty。 | 0/0 (结果为 nan) |
i 或 j | 虚数单位 sqrt−1。 | complex_num = 3 + 4i |
TRUE | 逻辑真(值为 1)。 | is_true = (5 > 3) |
FALSE | 逻辑假(值为 0)。 | is_false = (5 < 3) |
eps | 浮点相对精度(机器 epsilon)。表示 1.0 与大于 1.0 的下一个浮点数之间的距离。 | eps (通常约为 2.2204times10−16) |
nargin | 函数输入参数的数量。在函数内部使用。 | function output = myFunction(a, b) <br> if nargin < 2, error('需要至少两个输入参数'); end |
nargout | 函数输出参数的数量。在函数内部使用。 | function [out1, out2] = myOtherFunction(input) <br> if nargout == 1, out2 = []; end |
ans | 默认结果变量。当您没有为操作结果指定变量时,MATLAB 会将其存储在 ans 中。 | 2 + 3 (结果存储在 ans 中) |
7.变量命名
1.变量命名必须以字母开头,之后可以是任意字母,数字,下划线
正确示例: myVariable, data_2024, _tempValue (虽然以下划线开头是允许的,但通常不推荐,因为它可能与系统变量或特殊函数混淆)。
错误示例: 1stData (以数字开头), my-variable (包含连字符), total price (包含空格)。
2.变量名字母区分大小写
3.变量名不超过31个字符
8.矩阵
矩阵构造 | zeros(m, n) | 创建 m x n 的全零矩阵 | zeros(3, 2) |
ones(m, n) | 创建 m x n 的全一矩阵 | ones(2, 4) | |
eye(n) | 创建 n x n 的单位矩阵 | eye(3) | |
rand(m, n) | 创建 m x n 的 (0,1) 均匀分布随机矩阵 | rand(2, 2) | |
randn(m, n) | 创建 m x n 的标准正态分布随机矩阵 | randn(1, 3) | |
randi(imax, m, n) | 创建 m x n 的 1 到 imax 随机整数矩阵 | randi(10, 2, 2) | |
diag(v) | 从向量 v 创建对角矩阵 | diag([1 2 3]) |
1. 全零矩阵
全零矩阵 是指所有元素都为零的矩阵。
函数: zeros()
示例:
创建一个 3x4 的全零矩阵
A = zeros(3, 4)
A =
0 0 0 0
0 0 0 0
0 0 0 0
创建一个与现有矩阵 B 大小相同的全零矩阵
B = [1 2; 3 4; 5 6];
C = zeros(size(B))
C =
0 0
0 0
0 0
1. 全一矩阵
全一矩阵 是指所有元素都为一的矩阵。
函数: ones()
示例:
创建一个 2x5 的全一矩阵
D = ones(2, 5)
D =
1 1 1 1 1
1 1 1 1 1
创建一个与向量 V 形状相同的全一矩阵
V = [1 2 3];
E = ones(size(V))
E =
1 1 1
1. 对角矩阵
对角矩阵 可以通过两种方式生成:从一个向量创建,或者从一个现有矩阵中提取对角线元素。
函数: diag()
示例:
从向量创建对角矩阵
myVector = [10 20 30];
F = diag(myVector)
F =
10 0 0
0 20 0
0 0 30
从矩阵中提取主对角线元素
G_matrix = [1 2 3; 4 5 6; 7 8 9];
G_diag = diag(G_matrix)
G_diag =
1
5
9
1. 行串联矩阵
horzcat 函数用于将多个数组按行方向(水平)并排连接起来。这意味着所有参与连接的数组必须具有相同的行数。
• 函数形式: C = horzcat(A1, A2, ...)

1. 列串联矩阵
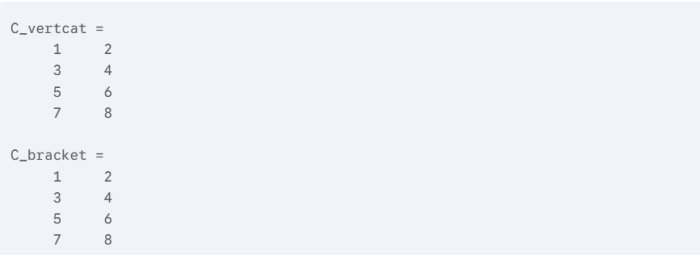
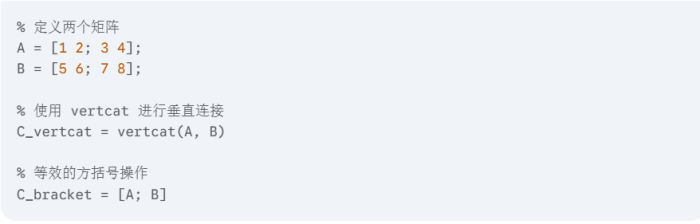
垂直连接 (vertcat)
vertcat 函数用于将多个数组按列方向(垂直)堆叠起来。这意味着所有参与连接的数组必须具有相同的列数
• 函数形式: C = vertcat(A1, A2, ...)

1. 单位矩阵
单位矩阵 是一个方阵,其主对角线上的元素均为一,其余元素均为零。
函数: eye()
Matlab
创建一个 4x4 的单位矩阵
J = eye(4)
J =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
创建一个 2x3 的非方单位矩阵(主对角线为1)
K = eye(2, 3)
K =
1 0 0
0 1 0
1. 生成数值序列
运算符: start:step:end 或 start:end (步长默认为 1)
函数: linspace() (生成等间隔点)
示例:
Matlab
生成从 1 到 10,步长为 1 的整数序列
L = 1:10
L =
1 2 3 4 5 6 7 8 9 10
生成从 0 到 100,步长为 5 的序列
M = 0:5:100
M =
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100
9.矩阵元素表示
1. 第二行所有列
要获取矩阵的第二行所有列,您可以使用 2 作为行索引,并使用冒号 : 作为列索引,表示“所有”。


1. 第三列所有行
要获取矩阵的第三列所有行,您可以使用冒号 : 作为行索引,并使用 3 作为列索引


1. 第一行第二列
要获取矩阵的第一行第一列2列的元素(1,1:2)
10.常用矩阵运算函数
类别 | 运算符/函数 | 描述 | 示例 |
基本算术 | + | 逐元素加法 | A + B |
- | 逐元素减法 | A - B | |
.* | 逐元素乘法 (Hadamard 积) | A .* B | |
* | 矩阵乘法 (点积) | A * B | |
./ | 逐元素右除 | A ./ B | |
\ | 左除 / 矩阵除法 (解 Ax=B) | x = A \ B | |
/ | 右除 (解 xA=B) | x = B / A | |
.^ | 逐元素幂 | A .^ 2 | |
^ | 矩阵幂 (方阵) | A ^ 2 | |
共轭转置 | A' | ||
.' | 非共轭转置 | A.' |
1.加法
A = [1 2; 3 4]; B = [5 6; 7 8];
C = A + B
% C =
% 6 8
% 10 12
2.减法
A = [1 2; 3 4]; B = [5 6; 7 8];
C = A - B
% C =
% -4 -4
% -4 -4
3.乘法
A = [1 2; 3 4]; B = [5 6; 7 8];
C = A * B
% C =
% 19 22
% 43 50
11.关系运算P53页
关系运算符 | 函数形式 | 描述 |
#ERROR! | eq(A, B) | 相等 (equal to) |
~= | ne(A, B) | 不等 (not equal to) |
< | lt(A, B) | 小于 (less than) |
<= | le(A, B) | 小于或等于 (less than or equal to) |
> | gt(A, B) | 大于 (greater than) |
>= | ge(A, B) | 大于或等于 (greater than or equal to) |
1.大于
A = [1 5 3];
B = [2 5 2];
result = A > B
% result =
% 0 0 1
小于类似
12.逻辑运算
2.举例
A= 0 1 2
3 0 5
6 5 0
B= 3 2 2
4 5 5
0 9 0
~A&B如何计算
首先将A和B转换一下成逻辑数组(有0为0,非0为1)
A= 0 1 1
1 0 1
1 1 0
B= 1 1 1
1 1 1
0 1 0
~A为对A取反
A= 1 0 0
0 1 0
0 0 1
&为与(全1为1)
~A&B=1 0 0
0 1 0
0 0 0
|为或
~A|B= 1 1 1
1 1 1
0 1 1
结论:A|(~A)为全1矩阵
A&(~A)为全0矩阵
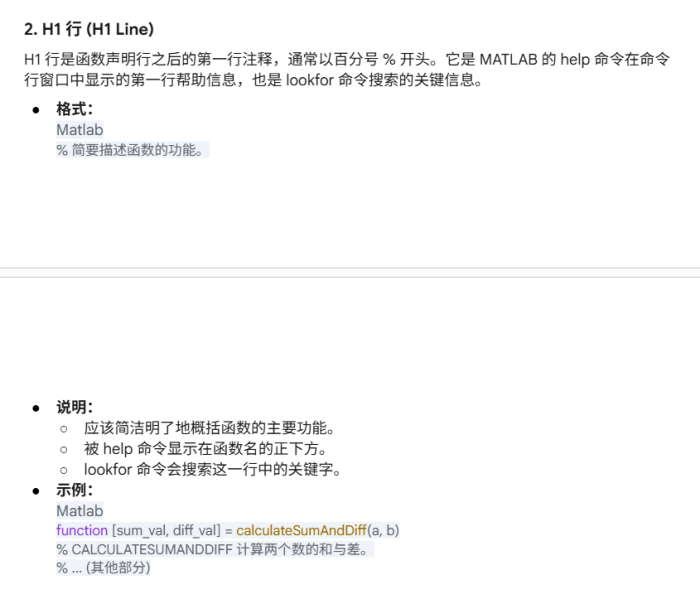
13.函数文件
一个典型的 MATLAB 函数文件(.m 文件)通常按以下顺序组织:




14.常用图形修饰函数及说明
类别 | 函数/命令 | 描述 | 示例 |
标题与标签 | title('文本') | 设置图表标题 | title('销售额趋势') |
axis([Xmin,Xmax,Ymin,Ymax]) | x,y坐标轴范围的调整 | ||
xlabel('文本') | 设置 x 轴标签 | xlabel('月份') | |
ylabel('文本') | 设置 y 轴标签 | ylabel('金额 ($)') | |
legend('系列1', ...) | 添加图例以标识数据系列 | legend('实际', '预测', 'Location', 'best') | |
坐标轴控制 | grid on | 显示网格线 | grid on |
grid off | 关闭网格线 | grid off | |
文本与标注 | gtext('string') | 在图形中添加文本 |
15.图形窗口控制函数及说明
函数/命令 | 描述 | 示例 |
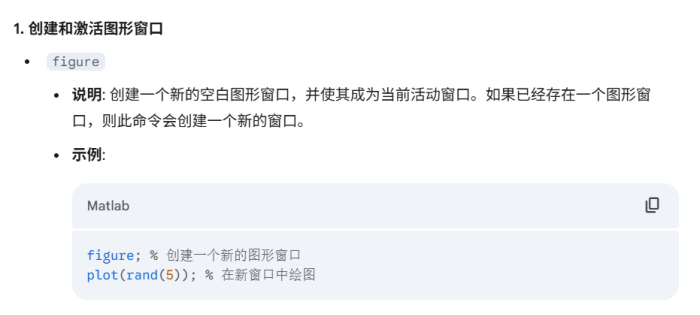
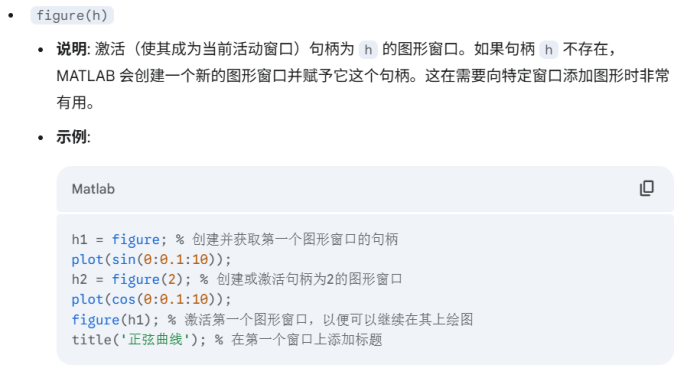
figure | 创建一个新的空白图形窗口,并使其成为当前活动窗口。 | figure; |
figure(n) | 激活(使其成为当前活动窗口)编号为 n 的图形窗口。如果编号 n 的窗口不存在,则创建一个新窗口并赋予此编号。 | figure(1); % 激活或创建第一个窗口 |
clf | 清空当前图形窗口中的所有图形对象(如线条、文本),但窗口本身保持打开。 | plot(x, y); clf; plot(a, b); |
hold on | 保持当前坐标区的内容。后续绘图命令将添加到现有图中,而不是清除它。 | plot(x1, y1); hold on; plot(x2, y2, 'r--'); |
hold off | 释放图形保持状态(默认状态)。后续绘图命令将清除当前坐标区的内容。 | hold off; |
subplot(m, n, p) | 将当前图形窗口划分为 m 行 n 列的网格,并选择第 p 个子图作为当前的绘图区域。 | subplot(2, 2, 1); % 在2x2网格的左上角绘图 |
close | 关闭当前活动的图形窗口。 | close; |
close all | 关闭所有打开的图形窗口。 | close all; |
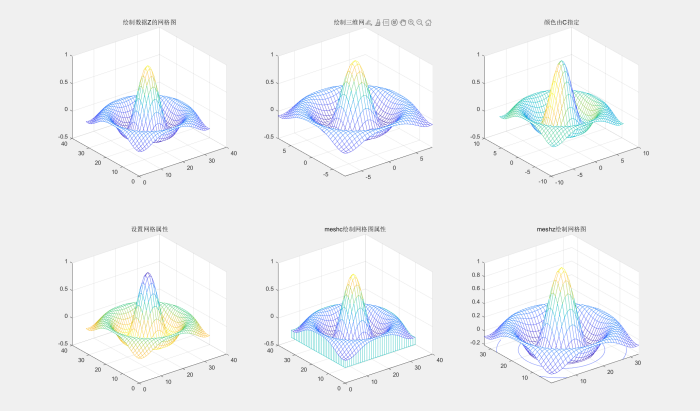
16.三维网格图
clear all;
[X,Y]=meshgrid(-8:.5:8);
R=sqrt(X.^2+Y.^2)+eps;
Z=sin(R)./R;
subplot(231);mesh(Z);
title('绘制数据Z的网格图');
subplot(232);mesh(X,Y,Z);
axis([-8 8 -8 8 -0.5 1]);
title('绘制三维网格图');
C=gradient(Z);
subplot(233);mesh(X,Y,Z,C);
title('颜色由C指定');
C=del2(Z);
subplot(234);mesh(Z,C,'FaceLighting','gouraud','LineWidth',0.3);
title('设置网格属性');
subplot(235);meshz(Z);
title('meshc绘制网格图属性');
subplot(236);meshc(Z);
title('meshz绘制网格图');
clear all; % 清除工作区中的所有变量。
% 创建二维网格数据 (X, Y)
[X,Y]=meshgrid(-8:.5:8);
% meshgrid 函数用于生成二维网格坐标。
% -8:.5:8 表示从 -8 到 8,步长为 0.5 的等差数列。
% X 矩阵的每一行都是这个数列的副本,Y 矩阵的每一列都是这个数列的副本。
% 这样,(X(i,j), Y(i,j)) 就构成了网格点坐标。
% 计算 Z 值:这是一个二维Sinc函数 (sin(R)/R)
R=sqrt(X.^2+Y.^2)+eps;
% 计算每个网格点到原点 (0,0) 的距离 R。
% X.^2 表示 X 中每个元素的平方,Y.^2 同理。
% sqrt() 是平方根函数。
% +eps 是为了避免当 R 为 0 时出现除以零的错误。eps 是 MATLAB 中的机器浮点精度,一个非常小的正数。
Z=sin(R)./R;
% 计算 Z 值。sin(R) 是对 R 中每个元素求正弦。
% ./ 是逐元素除法。
% --- 子图 1: 基本网格图 ---
subplot(231); % 创建一个 2x3 的子图网格,并激活第一个子图(位于第一行第一列)。
mesh(Z); % 绘制数据 Z 的网格图。
% 当 mesh 只有一个输入参数 Z 时,它默认将 X 和 Y 坐标设置为 Z 的行索引和列索引。
title('绘制数据Z的网格图'); % 为当前子图添加标题。
% --- 子图 2: 带自定义坐标轴的三维网格图 ---
subplot(232); % 激活第二个子图(位于第一行第二列)。
mesh(X,Y,Z); % 绘制三维网格图,使用 X, Y 作为坐标,Z 作为高度。
axis([-8 8 -8 8 -0.5 1]);
% 设置当前坐标轴的显示范围。
% [-8 8] 设置 X 轴的范围。
% [-8 8] 设置 Y 轴的范围。
% [-0.5 1] 设置 Z 轴的范围。这使得图形 Z 轴的显示更加聚焦和美观。
title('绘制三维网格图'); % 为当前子图添加标题。
% --- 子图 3: 颜色由梯度指定的三维网格图 ---
C=gradient(Z); % 计算 Z 的数值梯度。
% gradient 函数计算 Z 沿每个维度的偏导数的近似值。
% 这里返回的 C 是一个与 Z 大小相同的矩阵,其值代表 Z 的变化率。
subplot(233); % 激活第三个子图(位于第一行第三列)。
mesh(X,Y,Z,C); % 绘制三维网格图,并将颜色映射到矩阵 C 的值。
% 此时,网格的颜色不再仅仅由 Z 的高度决定,而是由 C 的值决定,呈现出 Z 变化趋势的视觉效果。
title('颜色由C指定'); % 为当前子图添加标题。
% --- 子图 4: 设置网格属性并用拉普拉斯算子颜色映射 ---
C=del2(Z); % 计算 Z 的离散拉普拉斯算子。
% del2 函数计算 Z 的二维离散拉普拉斯算子(数值二阶导数)。
% 这是一个常用于图像处理和物理模拟的算子,通常表示曲率或扩散。
subplot(234); % 激活第四个子图(位于第二行第一列)。
mesh(Z,C,'FaceLighting','gouraud','LineWidth',0.3);
% 绘制网格图,并进行以下设置:
% 第一个参数 Z:作为高度数据。
% 第二个参数 C:作为颜色映射数据。
% 'FaceLighting','gouraud':设置网格面的着色方式为 Gouraud 光照。
% Gouraud 着色是一种平滑的着色技术,通过在顶点计算光照并在面内部插值颜色,使曲面看起来更光滑。
% 'LineWidth',0.3:设置网格线的宽度为 0.3 点。使网格线显得更细。
title('设置网格属性'); % 为当前子图添加标题。
% --- 子图 5: meshz 绘制带底座的网格图 ---
subplot(235); % 激活第五个子图(位于第二行第二列)。
meshz(Z); % 绘制网格图,并在网格底部添加一个“幕布”或“底座”,从网格的边缘延伸到 z=0 平面。
% 这有助于更好地可视化曲面与基准平面的关系。
title('meshz绘制网格图属性'); % 为当前子图添加标题。
% --- 子图 6: meshc 绘制带等高线的网格图 ---
subplot(236); % 激活第六个子图(位于第二行第三列)。
meshc(Z); % 绘制网格图,并在 xy 平面上同时绘制等高线图。
% 等高线是 Z 值的投影,显示了 Z 值在不同高度的分布。
% 这结合了三维曲面和二维等高线的优点,提供了更全面的信息。
title('meshc绘制网格图'); % 为当前子图添加标题。
17.sinks、sources模块
sink中注意 to workspace 、display、scope、record
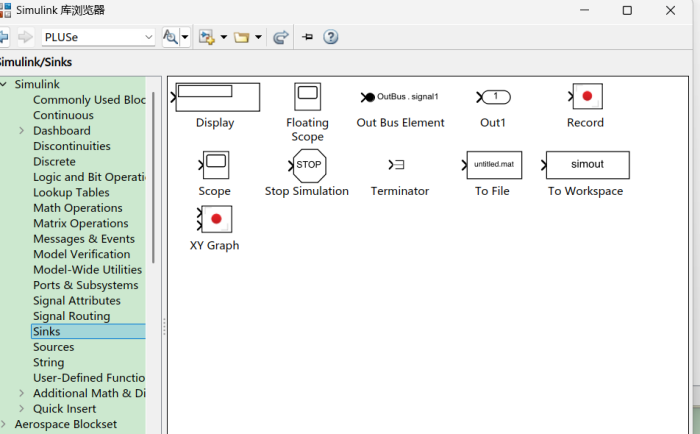
sources中注意in、from workspace、constant、step、sine wave、pulse generator
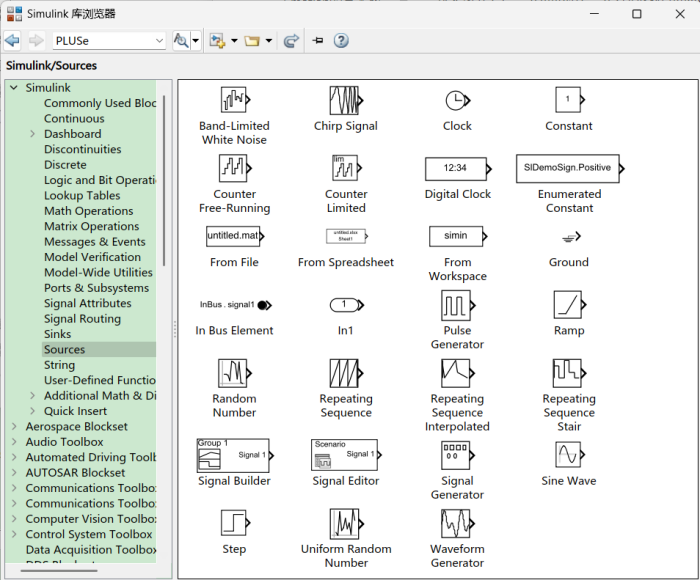
18.输入信号、激励、系统状态、输出信号、或响应
把外界对系统产生作用的物理量称为输入信号或激励,把系统内部存储的能量称为系统状态,而将系统对外界的作用物理量称为系统的输出信号或响应。
静态系统(无记忆系统),动态系统(记忆系统)
现在激励和状态能够影响系统的过去(非因果系统)
A. 简单子系统 (Simple Subsystem)
简单子系统
是系统中最基础、最独立的组成部分。它执行一项特定的功能,并且其操作不依赖于复杂的条件。你可以把它想象成一个基本的功能模块,只要被激活,就会执行它被设计好的任务。
B. 条件子系统 (Conditional Subsystems)
条件子系统
则更为复杂。它们的运行取决于是否满足某些特定条件。它们不会盲目执行,而是会根据“如果”或“当”某些条件达成时才进行操作。
a. 使能子系统 (Enabling Subsystem)
使能子系统
由一个“使能”信号或条件来控制。它只有当这个使能条件为真或激活时才开始运行或允许其功能执行。如果使能条件不满足,无论其他输入如何,该子系统都将保持非活动状态。
b. 触发子系统 (Triggered Subsystems)
触发子系统
旨在响应输入信号的特定事件或变化(称为“触发”)来执行其功能。它们不会持续运行,而是会等待特定的信号转换。
以下是不同类型的边沿触发:
上升沿触发 (Rising Edge Trigger): 这种子系统在输入信号从低电平转换到高电平的瞬间激活(就像打开电灯开关一样)。这是信号“上升”的那一刻。
下降沿触发 (Falling Edge Trigger): 这种子系统在输入信号从高电平转换到低电平的瞬间激活(就像关闭电灯开关一样)。这是信号“下降”的那一刻。
双边沿触发 (Dual-Edge Trigger / Double-Edge Trigger): 这种子系统在输入信号的上升沿和下降沿都会激活。它对信号状态的任何变化(无论是上升还是下降)都会做出响应。
do-while先执行一次再判断条件和循环次数
21.封闭系统方法优点P144:
1.将子系统内众多模块参数对话框集成为一个单独的对话框,用户可对该对话框输入不同参数值
2.可把个别模块描述和帮助集成在一起
3.可以制作该子系统的Icon图标,直观表示模块用途。
22.噪声种类
- 单频噪声 :是指在特定的单一频率上持续出现的噪声。例如,在一个通信系统中,如果有某个特定频率的干扰源,如附近的电台发射的固定频率信号,就可能引入单频噪声,它会持续在该频率处干扰信号的传输,影响信号的质量和准确性。
- 脉冲噪声 :是一种突发性的噪声,其特点是持续时间较短但幅度较大,通常呈现为脉冲状或尖峰状。比如,在电力系统中,当开关电器动作时,可能会产生脉冲噪声,这种噪声会瞬间干扰通信线路中的信号,造成信号的失真或错误。
- 起伏噪声(白噪声) :白噪声是一种功率谱密度在整个频域内均匀分布的噪声,即其在各个频率上的功率相同。起伏噪声是指其幅度随时间随机起伏变化的噪声,白噪声就是一种典型的起伏噪声。例如,在环境声音中,我们经常会听到的嘈杂声、电视雪花等,都包含了白噪声成分,它会持续影响信号的传输,在各种通信和电子系统中普遍存在。
23.信源产生函数
- randerr 函数 :在 MATLAB 中,randerr 函数用于产生随机的二进制错误序列。其基本语法为 randerr(len,n),其中 len 是需要产生错误序列的位数,n 是错误概率的倒数,表示平均在 n 个比特中出现 1 个错误。例如,randerr(1000,10)将产生一个长度为 1000 的二进制序列,其中大约有 100 个错误比特(即 1 的位置)。
- randi 函数 :用于生成均匀分布的伪随机整数。其基本语法为 randi(imax,sz1,...,szN),其中 imax 是生成整数的最大值,sz1,...,szN 指定生成数组的大小。例如,randi(10,2,3)将生成一个 2 行 3 列的矩阵,其中每个元素都是 1 到 10 之间的随机整数,可以用来模拟数字信号源的输出,如表示数字信号的电平状态等。
- randsrc 函数 :用于生成随机信号。其基本语法为 randsrc(m,n,alphabet,prob),其中 m 和 n 指定输出矩阵的大小,alphabet 是输出信号的可能值组成的向量,prob 是对应的概率向量。例如,randsrc(1,10,[-3 -1 1 3],[0.2 0.3 0.3 0.2])将生成一个 1 行 10 列的向量,其元素从 [-3,-1,1,3] 中随机选取,且每个元素取对应值的概率分别为 0.2、0.3、0.3、0.2,可用于模拟具有特定取值和概率分布的离散信号源。
24. 信道函数
- awgn 函数 :全称为 “Additive White Gaussian Noise”(加性高斯白噪声)函数,用于给信号添加高斯白噪声,模拟信号在传输过程中受到的热噪声等随机干扰。其基本语法为 y = awgn(x,snr,signalpower),其中 x 是输入信号,snr 是信噪比,以分贝(dB)为单位,signalpower 指定信号的功率,若省略则默认信号的平均功率为 0dBW。例如,假设有一个信号 x = sin(2 * pi * 100 * t),t 为时间向量,要给该信号添加信噪比为 20dB 的高斯白噪声,可以使用 y = awgn(x,20),然后可以通过绘制原始信号和加噪信号的波形图,观察加噪后信号的变化情况,以分析噪声对信号的影响。
简答题
1.P179对输入的锯齿波进行叠加高斯白噪声
t=0:.1:10;
x=sawtooth(t); % 这一行生成一个锯齿波形。
y=awgn(x,10,'measured'); % 这一行向信号 'x' 添加了加性高斯白噪声 (AWGN)。 信噪比 (SNR)为10(dB)。
plot(t,x,t,y) %绘制原信号和输出信号
legend(‘原始信号’,'叠加高斯白噪声信号');
2.P254低通滤波器
1.求滤波器最小阶数和3dB截止频率
[n,Wn]=buttord(Wp,Ws,Rp,Rs)返回符合要求的数字滤波器的最小阶次n和滤波器的固有频率Wn(3dB),Wp为截止频率,Ws为阻带频率,Rp允许最大哀减,Rs阻带应该达到的最小衰减。对于带通和带阻Wp Ws为1x2的向量,低通和高通Ws和Wp为标量,wp ws为归一化频率,为对应抽样的频率的一半。
clear all; % 清除工作区中的所有变量
Rp = 1; % 通带最大衰减为 1 dB
Rs = 30; % 阻带最小衰减为 30 dB
% 利用 buttord 计算模拟巴特沃斯滤波器的最小阶数 n 和归一化截止频率 fn
% 通带频率为 [9 10] Hz,阻带频率为 [8 11] Hz,单位为 Hz
[n, fn] = buttord([9 10], [8 11], Rp, Rs, 's'); % 's' 表示模拟滤波器设计
% 将归一化频率(Hz)转换为模拟角频率(rad/s),Wn 是角频率向量
Wn = 2 * pi * fn;
% 使用 butter 函数设计巴特沃斯模拟滤波器,返回分子系数 b 和分母系数 a
% b 和 a 分别是滤波器的分子和分母多项式系数
[b, a] = butter(n, Wn, 's'); % 's' 表示模拟滤波器设计
% 频率向量(Hz),用于频率响应绘图
f = 0��10000;
% 构造复频域变量 s = j2pi*f
s = 1j * 2 * pi * f;
% 计算频率响应 H(s) = B(s) / A(s)
% polyval 将多项式 b 和 a 应用于 s 向量,得到频率响应
Hs = polyval(b, s) ./ polyval(a, s);
% 绘图部分
figure(1);
% 幅度响应图(单位:dB)
subplot(2,1,1);
plot(f, 20 * log10(abs(Hs))); % 20*log10 为幅度转dB
axis([0 10000 -40 1]); % 设置坐标轴范围
xlabel('频率/Hz'); ylabel('幅度/dB');
grid on;
% 相位响应图(单位:弧度)
subplot(2,1,2);
plot(f, angle(Hs)); % 计算相位响应
xlabel('频率/Hz'); ylabel('相角/rad');
grid on;
% 显示滤波器参数
disp('滤波器阶数和截止频率:');
disp(n); % 显示滤波器阶数
disp(Wn); % 显示角频率截止频率(rad/s)
disp(b); % 显示滤波器分子系数
disp(a); % 显示滤波器分母系数
计算3dB固有频率
% 设计参数
fp = [9e3, 10e3]; % 通带上下边频 (Hz)
fs = [8e3, 11e3]; % 阻带上下边频 (Hz)
Ap = 1; % 通带最大衰减 (dB)
As = 30; % 阻带最小衰减 (dB)
% 转换为角频率 (rad/s)
wp = 2pifp;
ws = 2pifs;
% 计算阶数和自然频率
[n, wn] = buttord(wp, ws, Ap, As, 's');
% 设计巴特沃斯带通滤波器
[b, a] = butter(n, wn, 'bandpass', 's');
% 转换自然频率到Hz
wn_Hz = wn / (2*pi);
% 显示结果
disp(['滤波器阶数: n = ', num2str(n)]);
disp(['3dB截止频率: ', num2str(wn_Hz(1)/1e3), ' kHz 和 ', num2str(wn_Hz(2)/1e3), ' kHz']);
% 保存滤波器系数
save('ButterworthBPF.mat', 'b', 'a', 'n', 'wn_Hz');
2.求传递函数
3.FFT/IFFT/IFFTSHIFT
操作 |
FFT |
IFFT |
fftshift |
ifftshift |
假设某复合周期型信号,为两个信号的合成,其中包括一个周期为20Hz、幅值0.5、相位0的正弦波信号和一个周期为40Hz、幅值2、相位0的余弦波信号。
对于该信号的采样率为100Hz,傅里叶变换长度为256。
% clear all;
% 清除 MATLAB 工作区中的所有变量。
clear all;
% f1=20;
% 定义第一个正弦波的频率为 20 Hz。
f1 = 20;
% f2=40;
% 定义第二个余弦波的频率为 40 Hz。
f2 = 40;
% fs=100;
% 定义采样频率为 100 Hz。这意味着每秒采集 100 个样本。
fs = 100;
% T=2;
% 定义信号的总时长为 2 秒。
T = 2;
% dt=1/fs;
% 计算采样时间间隔。它是采样频率的倒数。
dt = 1/fs;
% t=0:dt:T-dt;
% 创建时间向量。它从 0 开始,以 dt 为步长递增,直到 T-dt。
% 这样做是为了确保时间向量的长度与信号的样本数一致,避免最后一个点超出总时长。
t = 0:dt:T-dt;
% A1=0.5;
% 定义第一个正弦波的幅度为 0.5。
A1 = 0.5;
% A2=2;
% 定义第二个余弦波的幅度为 2。
A2 = 2;
% N = 256; % FFT点数
% 定义进行快速傅里叶变换 (FFT) 的点数。通常选择 2 的幂次方以提高 FFT 算法的效率。
N = 256;
% % 生成信号
% x=A1sin(2pif1t)+A2cos(2pif2t);
% 根据定义的频率、幅度和时间向量生成合成信号 'x'。
% 这是一个由一个正弦波和一个余弦波叠加而成的信号。
x=A1sin(2pif1t)+A2cos(2pif2t);
% % 计算FFT
% X = fft(x, N);
% 对信号 'x' 进行 N 点的快速傅里叶变换。
% 'X' 将包含信号在频域的复数值表示。
X = fft(x, N);
% df = fs/N; % 频率分辨率 (Hz)
% 计算频率分辨率。它表示频域中相邻数据点之间的频率间隔。
df = fs/N;
% f = (0:N-1)df;
% 创建频率向量。它从 0 开始,以 df 为步长递增,直到 (N-1)df。
% 这个向量对应于 fft 函数输出的频率轴,从 0 到奈奎斯特频率 (fs/2) 再到负频率部分。
f = (0:N-1)*df;
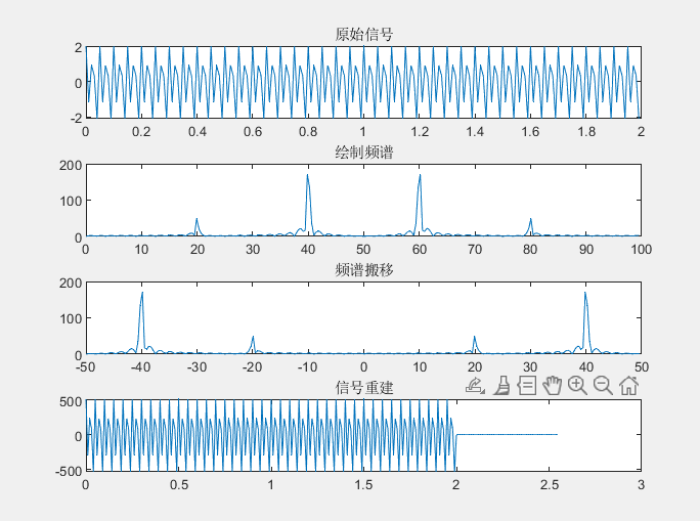
绘制原始信号
% subplot(411);
% 创建一个 4x1 的子图布局,并在第一个位置 (411) 绘制图形。
subplot(411);
% 绘制原始信号 'x' 随时间 't' 的变化。
plot(t, x);
% 为子图设置标题为“原始信号”。
title('原始信号');
绘制频谱
% subplot(412);
% 在 4x1 子图布局的第二个位置 (412) 绘制图形。
subplot(412);
% 绘制 FFT 结果 'X' 的幅度谱 (abs(X)) 随频率 'f' 的变化。
% 由于 fft 函数的输出是双边谱(包含正负频率,但负频率部分是正频率的共轭),
% 默认的频率轴是从 0 到 fs。你会看到在 f1 和 f2 处有峰值,以及它们在 fs-f1 和 fs-f2 处的镜像峰值。
plot(f, abs(X));
% 为子图设置标题为“绘制频谱”。
title('绘制频谱');
计算并绘制频谱搬移
% Y = fftshift(X);
% 使用 'fftshift' 函数将 FFT 结果 'X' 的零频率分量(直流分量)移到频谱的中心。
% 这使得频谱图看起来更符合我们对正负频率的直观理解。
Y = fftshift(X);
% n2 = -N/2 : (N/2 - 1);
% 创建一个新的索引向量,用于生成以零为中心的频率轴。
% 对于偶数 N,范围是 -N/2 到 N/2 - 1。
n2 = -N/2 : (N/2 - 1);
% f2 = df * n2;
% 根据新的索引和频率分辨率创建以零为中心的频率向量。
% 这个频率向量将从 -fs/2 到 fs/2 - df。
f2 = df * n2;
% subplot(413);
% 在 4x1 子图布局的第三个位置 (413) 绘制图形。
subplot(413);
% 绘制经过 'fftshift' 后的频谱 'Y' 的幅度谱随以零为中心的频率 'f2' 的变化。
% 此时,你会看到在 -f2, -f1, f1, f2 处有对称的峰值。
plot(f2, abs(Y));
% 为子图设置标题为“频谱搬移”。
title('频谱搬移');
信号重建
% x_recon=Nifft(ifftshift(Y),N);
% 通过对经过 'fftshift' 处理的频谱 'Y' 进行逆快速傅里叶变换 (IFFT) 来重建原始信号。
% 注意:这里的 'N' 因子是必需的,因为 FFT 和 IFFT 默认有 1/N 或 N 的缩放因子,
% 具体取决于软件实现。在 MATLAB 中,'ifft' 默认会除以 N,所以为了得到原始信号的幅度,
% 通常需要乘以 N。
x_recon = N * ifft(ifftshift(Y), N);
% t_recon=(0:N-1)dt;
% 创建用于重建信号的时间向量。这里我们使用 FFT 点数 'N' 来定义重建信号的时间长度。
t_recon = (0:N-1)dt;
% subplot(414);
% 在 4x1 子图布局的第四个位置 (414) 绘制图形。
subplot(414);
% 绘制重建后的信号 'x_recon' 随时间 't_recon' 的变化。
% 理想情况下,这个图应该与第一个子图(原始信号)非常相似。
plot(t_recon, real(x_recon)); % 使用 real() 确保只绘制实部,因为 IFFT 结果可能因浮点精度而有微小虚部。
% 为子图设置标题为“信号重建”。
title('信号重建');
填空题
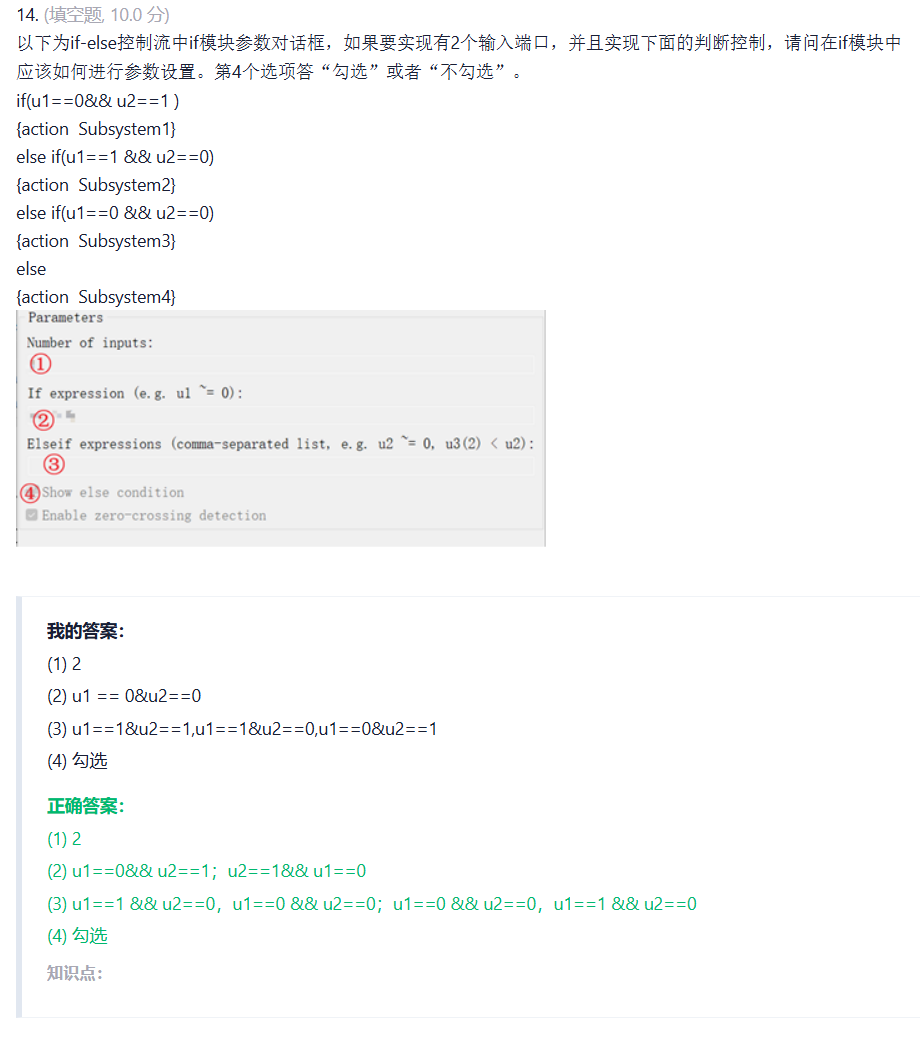
1.if-else
2.sin/cos信号
dt = 1e-5; % 时间步长(采样间隔),单位为秒(s),即 10 微秒(10e-6 s)
T = 3 * 1e-3; % 仿真总时长,单位为秒(s),即 3 毫秒(3e-3 s)
t = 0:dt:T; % 时间向量,从 0 到 T,步长为 dt,用于生成信号的时间轴
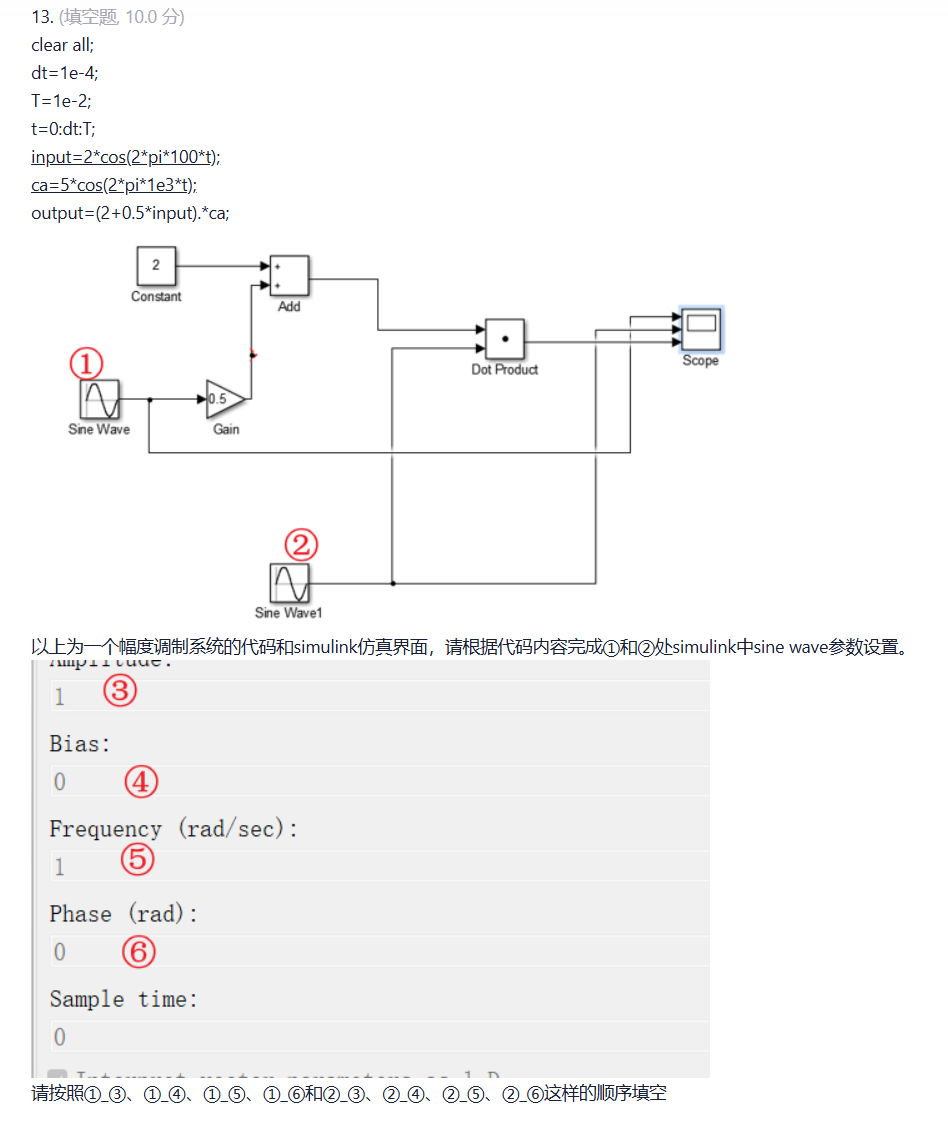
bias代表sin、cos后面还有个加减该值才不为0例如cos(2*pi+4)则为4、frequency频率、phase相位
问题
触发子系统
上升沿触发
下降沿触发
双边沿触发
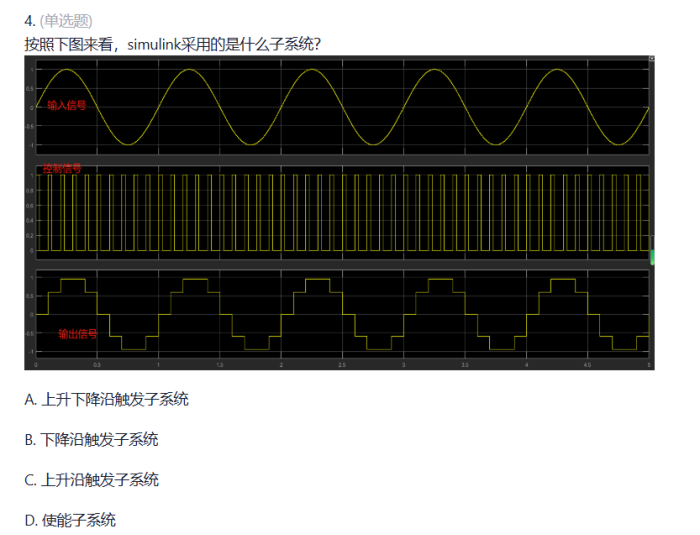
求传递函数

